![[Java, C++] AVL 트리](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbxbvfR%2FbtsOeDP00sn%2Fr7hLrQsPnII0NTpMKgsvn0%2Fimg.png)


본 게시글은 학부 강의 '자료구조', 온라인 강의 'Honglab Data Structure(https://www.honglab.ai/)' 그리고 강의 교재 '자바와 함께하는 자료구조의 이해'의 내용들을 바탕으로 이해한 내용을 정리하였습니다.
AVL 트리(Hight Balanced Binary Trees)
- AVL 트리는 Adelson-Velskii & Landis Tree 라고도 한다. 만든 사람의 이름을 땄다.
- AVL 트리는 트리가 한쪽으로 치우치는 것을 방지하여 트리 높이의 균형을 유지
- 균형(Balanced) 이진 트리 : 탐색, 삽입, 삭제 연산의 수행 시간 O(logn) 보장
AVL 트리는 삽입이나 삭제로 인해 균형이 어긋나면 회전 연산을 통해 트리의 균형을 유지한다.
AVL 트리는 임의의 노드 x에 대해 x의 왼쪽 서브트리의 높이와 오른쪽 서브트리의 높이 차이가
1을 넘지 않는 이진 탐색 트리


n개의 노드를 가진 AVL 트리의 높이는 O(logn)
A(h) = 높이가 h인 AVL 트리를 구성하는 최소의 노드 수, A(1) = 1, A(2) = 2, A(3) = 4


- A(h) = A(h-1) + A(h-2) + 1, 단, A(0) = 0, A(1) = 1, A(2) = 2
- A(h) = F(h+2) - 1

AVL 트리의 회전 연산
AVL 트리에서 삽입 또는 삭제 연산을 수행할 때 트리의 균형을 유지하기 위해 LL-회전, RR-회전, LR-회전, RL-회전 연산 사용
회전 연산은 2개의 기본적인 연산으로 구현 - rotateRight(), rotateLeft()

private Node rotateRight(Node n) {
Node x = n.left;
n.left = x.right;
x.right = n;
n.height = tallerHeight(height(n.left), height(n.right)) + 1; // 높이 갱신
x.height = tallerHeight(height(x.left), height(x.right)) + 1; // 높이 갱신
return x; // 회전 후 x가 n의 이전 자리로 이동되었으므로
}
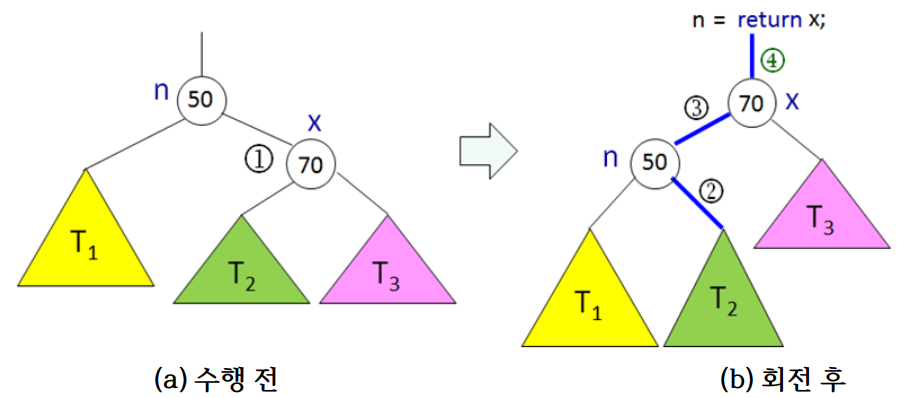
private Node rotateLeft(Node n) {
Node x = n.right;
n.right = x.left;
x.left = n;
n.height = tallerHeight(height(n.left), height(n.right)) + 1; // 높이 갱신
x.height = tallerHeight(height(x.left), height(x.right))) + 1; // 높이 갱신
return x;
}
LL-회전 : 우회전


RR-회전 : 좌회전

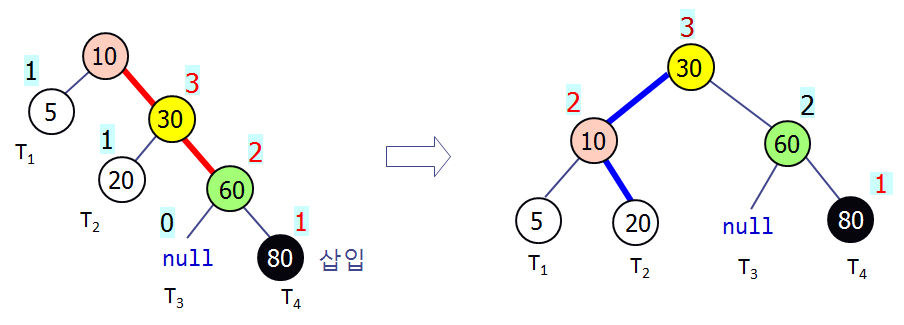
LL회전은 우회전, RR회전은 좌회전이다. 혼동하지 말 것.
직관적으로 보면
- LL(Left - Left) - 왼쪽 자식의 왼쪽에 문제가 생겼다. 불균형의 위치를 설명하는 것. 따라서 이 문제를 해결하기 위해 오른쪽으로 회전해야 한다.
- RR(Right - Right) - 오른쪽 자식의 오른쪽에 문제가 생겼다. 따라서 이 문제를 해결하려면 왼쪽으로 회전해야 한다.
LR-회전 : 이중회전


RL-회전 : 이중회전
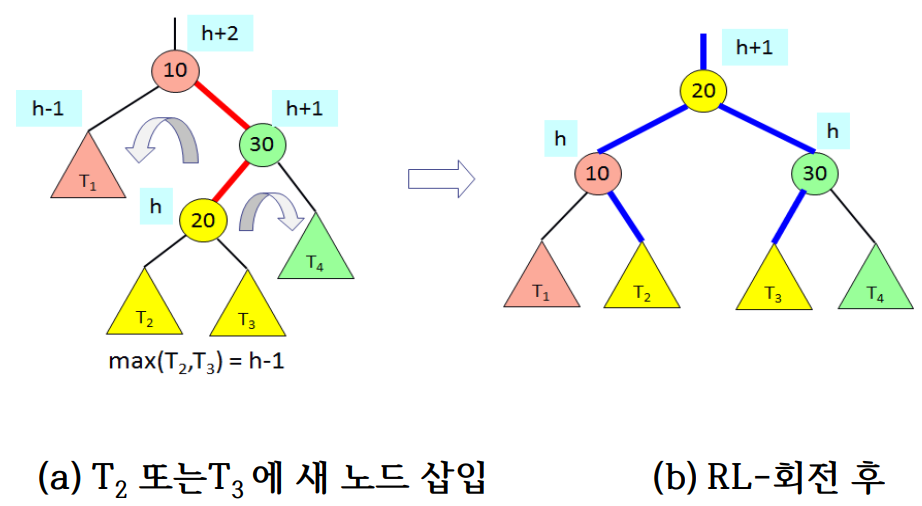

4 종류 회전의 공통점
- 회전 후의 트리들이 모두 같다.
- 각 회전 연산의 수행 시간 O(1)
회전이라는 말의 함정
'회전' 이라는 말에 혼동하지 말자. 노드들의 부모-자식 관계를 재배치하는 것을 단지 회전이라 표현하는 것.
전체적으로 보았을 때 트리를 돌리는 것처럼 보이기에.
회전 -> 균형 잡기 위한 재배치
Node class for AVL Tree
public class Node {
private Key id;
private Value name;
private int height;
private Node left, right;
public Node(Key newID, Value newName, int newHt) { // 생성자
id = newID;
name = newName;
height = newHt;
left = right = null;
}
}
삽입 연산
- 이진 탐색 트리의 삽입과 동일하게 새 노드 삽입
- 새 노드로부터 루트로 거슬러 올라가며 각 노드의 서브트리 높이 차이를 갱신
- 이때 가장 먼저 불균형이 발생한 노드를 발견하면, 이 노드를 기준으로 새 노드가 어디에 삽입되었는지에 따라 적절한 회전 연산을 수행
public void put(Key k, Value v) {root = put(root, k, v);}
private Node put(Node n, Key k, Value v) {
if (n == null) return new Node(k, v, 1);
int t = k.compareTo(n.id);
if (t < 0) n.left = put(n.left, k, v);
else if (t > 0) n.right = put(n.right, k, v);
else {
n.name = v; // k가 이미 트리에 있으므로 V만 갱신
return n;
}
n.height = tallerHeight(height(n.left), height(n.right)) + 1;
return balance(n); // 노드 n의 균형 점검 및 불균형을 바로 잡음
}
private Node balance(Node n) {
if (bf(n) > 1) { // 노드 n의 왼쪽 서브트리가 높아서 불균형 발생
if(bf(n.left) < 0) { // 노드 n의 왼쪽 자식노드의 오른쪽 서브트리가 높은 경우
n.left = rotateLeft(n.left);
}
n = rotateRight(n); // LL-회전
}
else if (bf(n) < -1) { // 노드 n의 오른쪽 서브트리가 높아서 불균형 발생
if (bf(n.right) > 0) { // 노드 n의 오른쪽 자식노드의 왼쪽 서브트리가 높은 경우
n.right = rotateRight(n.right);
}
n = rotateLeft(n); // RR-회전
}
return n;
}- Line 04 - Line 06은 LR-회전
- Line 10 - Line 12은 RL-회전
bf(n) : (노드 n의 왼쪽 서브트리 높이) - (오른쪽 서브트리 높이) 반환
private int bf(Node n) {
return height(n.left) - height(n.right);
}
private int height(Node n) {
if (n == null) return 0;
return n.height;
}
private int tallerHeight(int x, int y) {
if (x > y) return x;
else return y;
}
e.g.
30, 40, 100, 20, 10, 60, 70, 120, 110을 차례로 삽입하여 보자




삭제 연산
- 이진 탐색 트리에서와 동일한 삭제 연산 수행
- 삭제된 노드로부터 루트 방향으로 거슬러 올라가며 불균형이 발생한 경우 적절한 회전 연산 수행
- 회전 연산 수행 후에 부에서 불균형이 발생할 수 있고, 이러한 일이 반복되어 루트에서 회전 연산을 수행해야 하는 경우도 발생

삭제 후 불균형이 발생하면 반대쪽에 삽입이 이루어져 불균형이 발생한 것으로 취급
삭제된 노드의 부모 = p, p의 부모 = gp, p의 형제 = s
s의 왼쪽과 오른쪽 서브트리 중에서 높은 서브트리에 마치 새 노드를 삽입한 것으로 간주



수행 시간
- AVL 트리에서의 탐색, 삽입, 삭제 연산은 공통적으로 루트부터 탐색을 시작하여 최악의 경우에 이파리까지 내려가고, 삽입이나 삭제 연산은 다시 루트까지 거슬러 올라가야 한다.
- 트리를 1층 내려갈 때는 순환 호출하며, 1층을 올라갈 때 불균형이 발생하면 적절한 회전 연산을 수행, 각각은 O(1) 시간
- 탐색, 삽입, 삭제 연산의 수행 시간은 각각 AVL 트리의 높이에 비례 : O(logN)
- 다양한 실험 결과에 따르면, AVL 트리는 거의 정렬된 데이터를 삽입한 후에 랜덤 순서로 데이터를 탐색하는 경우 가장 좋은 성능을 보인다.
- 이진 탐색 트리 : 랜덤 순서의 데이터를 삽입한 후에 랜덤 순서로 데이터를 탐색하는 경우 가장 좋은 성능을 보인다.

'CS & AI > Data Structure' 카테고리의 다른 글
| [Java] 레드 블랙 트리 (1) | 2025.06.05 |
|---|---|
| [Java] 2-3 트리 (1) | 2025.06.03 |
| [Java, C++] 이진 탐색 트리(Binary Search Tree) (2) | 2025.05.26 |
| [Java] Union Find - 서로소 집합 (0) | 2025.05.12 |
| [Java, C++] 트리(Tree) (0) | 2025.05.12 |

나의 성장 드라마
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!
![[Java] 레드 블랙 트리](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FLipwU%2FbtsOo8nHKFL%2FmLbQTpEeQAeKyh0iEHeBJK%2Fimg.jpg)
![[Java] 2-3 트리](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FcxFEIk%2FbtsOmuTMFPw%2F8wxcF3pkcKa1Dg0ONtCTHk%2Fimg.png)
![[Java, C++] 이진 탐색 트리(Binary Search Tree)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FddtcWv%2FbtsOdDWqSvS%2FPXl5sY1mJArBvJIBG1Fhek%2Fimg.png)